Mister Muffin Blog

Sisyphus is a piece of software that I wrote as a member of a team from Jacobs University led by Prof. Dr. Andreas Nüchter. It managed to place our team first in this year's IEEE ICRA 2012 Virtual Manufacturing Automation Competition in all three rounds.

The goal was, to stack a given set of boxes of different length, height and width on a pallet in a way that achieved optimal volume utilization, center of mass and interlock of the boxes. Besides the cartesian placement of a box on the pallet, the only other degree of freedom was a 90° rotation of the box around a vertical axis.

Since the arrangement of boxes into a three dimensional container is NP hard (three dimensional orthogonal knapsack), I decided for a heuristic for an approximate solution.

The premise is, that there are many boxes of equal height which was the case in the test cases that were available from the 2011 VMAC.

Given this premise, my heuristic was, to arrange the boxes into layers of equal height and then stack these layers on top of each other. A set of boxes that would be left over or too little from the start to form its own full layer, would then be stacked on the top of the completed layers.

There is a video of how this looked like.

My code is now online on github and it even documented for everybody who is not me (or a potential future me of course).

This blog post is about the "interesting" parts of sisyphus. You can read about the overall workings of it in the project's README.

Python dict to XML and XML to Python dict

The evaluation program for the challenge is reading XML files and the pallet size and the list of articles with their sizes are also given in XML format. So I had to have a way to easily read article information from XML and to easily dump my data into XML format.

Luckily, all the XML involved was not making use of XML attributes at all, so the only children a node had, where other nodes. Thus, the whole XML file could be represented as an XML dictionary with keys being tagnames and the values being other dictionaries or lists or strings or integers.

The code doing that uses xml.etree.ElementTree and turns out to be very simple:

from xml.etree import ElementTree

def xmltodict(element):
    def xmltodict_handler(parent_element):
        result = dict()
        for element in parent_element:
            if len(element):
                obj = xmltodict_handler(element)
            else:
                obj = element.text
            if result.get(element.tag):
                if hasattr(result[element.tag], "append"):
                    result[element.tag].append(obj)
                else:
                    result[element.tag] = [result[element.tag], obj]
            else:
                result[element.tag] = obj
        return result
    return {element.tag: xmltodict_handler(element)}

def dicttoxml(element):
    def dicttoxml_handler(result, key, value):
        if isinstance(value, list):
            for e in value:
                dicttoxml_handler(result, key, e)
        elif isinstance(value, basestring):
            elem = ElementTree.Element(key)
            elem.text = value
            result.append(elem)
        elif isinstance(value, int) or isinstance(value, float):
            elem = ElementTree.Element(key)
            elem.text = str(value)
            result.append(elem)
        elif value is None:
            result.append(ElementTree.Element(key))
        else:
            res = ElementTree.Element(key)
            for k, v in value.items():
                dicttoxml_handler(res, k, v)
            result.append(res)
    result = ElementTree.Element(element.keys()[0])
    for key, value in element[element.keys()[0]].items():
        dicttoxml_handler(result, key, value)
    return result

def xmlfiletodict(filename):
    return xmltodict(ElementTree.parse(filename).getroot())

def dicttoxmlfile(element, filename):
    ElementTree.ElementTree(dicttoxml(element)).write(filename)

def xmlstringtodict(xmlstring):
    return xmltodict(ElementTree.fromstring(xmlstring))

def dicttoxmlstring(element):
    return ElementTree.tostring(dicttoxml(element))

Lets try this out:

>>> from util import xmlstringtodict, dicttoxmlstring
>>> xmlstring = "<foo><bar>foobar</bar><baz><a>1</a><a>2</a></baz></foo>"
>>> xmldict = xmlstringtodict(xmlstring)
>>> print xmldict
{'foo': {'baz': {'a': ['1', '2']}, 'bar': 'foobar'}}
>>> dicttoxmlstring(xmldict)
'<foo><baz><a>1</a><a>2</a></baz><bar>foobar</bar></foo>'

The dict container doesnt preserve order, but as XML doesnt require that, this is also not an issue.

Arranging items in layers

When it was decided, that I wanted to take the layered approach, it boiled down the 3D knapsack problem to a 2D knapsack problem. The problem statement now was: how to best fit small rectangles into a big rectangle?

I decided for a simple and fast approach as it is explained in Jake Gordon's blog article. There is a demo of his code and should the site vanish from the net, the code is on github. This solution seemed to generate results that were "good enough" while simple to implement and fast to execute. If you look very hard, you can still see some design similarities between my arrange_spread.py and his packer.js code.

Jake Gordon got his idea from Jim Scott who wrote an article of arranging randomly sized lightmaps into a bigger texture.

There is also an ActiveState Code recipe from 2005 which looks very similar to the code by Jake Gordon.

The posts of Jake Gordon and Jim Scott explain the solution well, so that I dont have to repeat it. Should the above resources go offline, I made backups of them here and here. There is also a backup of the ActiveState piece here.

Spreading items out

The algorithm above would cram all rectangles into a top-left position. As a result, there would mostly be space at the bottom and left edge of the available pallet surface. This is bad for two reasons:

1. the mass is distributed unequally
2. articles on the layer above at the bottom or left edge, are prone to overhang too much so that they tumble down

Instead all articles should be spread over the available pallet area, creating small gaps between them instead big spaces at the pallet borders.

Since articles were of different size, it was not clear to me from the start what "equal distribution" would even mean because it was obvious that it was not as simple as making the space between all rectangles equal. The spacing had to be different between them to accommodate for differently sized boxes.

The solution I came up with, made use of the tree structure, that was built by the algorithm that arranged the rectangles in the first place. The idea is, to spread articles vertically first, recursively starting with the deepest nodes and spreading them out in their parent rectangle. And then spreading them horizontally, spreading the upper nodes first, recursively resizing and spreading child nodes.

The whole recursion idea created problems of its own. One of the nicest recursive beauty is the following function:

def get_max_horiz_nodes(node):
    if node is None or not node['article']:
        return [], []
    elif node['down'] and node['down']['article']:
        rightbranch, sr = get_max_horiz_nodes(node['right'])
        rightbranch = [node] + rightbranch
        downbranch, sd = get_max_horiz_nodes(node['down'])
        ar = rightbranch[len(rightbranch)-1]['article']
        ad = downbranch[len(downbranch)-1]['article']
        if ar['x']+ar['width'] > ad['x']+ad['width']:
            return rightbranch, sr+[downbranch[0]]
        else:
            return downbranch, sd+[rightbranch[0]]
    else:
        rightbranch, short = get_max_horiz_nodes(node['right'])
        return [node] + rightbranch, short

get_max_horiz_nodes() traverses all branches of the tree that node has below itself and returns a tuple containing the list of nodes that form the branch that stretches out widest plus the list of nodes that are in the other branches (which are shorter than the widest).

Another interesting problem was, how to decide on the gap between articles. This was interesting because the number resulting of the subtraction of the available length (or width) and the sum of the articles lengths (or widths), was mostly not divisible by the amount of gaps without leaving a rest. So there had to be an algorithm that gives me a list of integers, neither of them differing by more than one to any other, that when summed up, would give me the total amount of empty space. Or in other words: how to divide a number m into n integer pieces such that each of those integers doesnt differ more than 1 from any other.

Surprisingly, generating this list doesnt contain any complex loop constructs:

>>> m = 108 # total amount
>>> n = 7 # number of pieces
>>> d,e = divmod(m, n)
>>> pieces = (e)*[(d+1)]+(n-e)*[d]
>>> print pieces
[16, 16, 16, 15, 15, 15, 15]
>>> sum(pieces) == m
True
>>> len(pieces) == n
True

You can test out the algorithms that arrange rectangles and spread them out by cloning the git and then running:

PYTHONPATH=. python legacy/arrange_spread.py

The results will be svg files test1.svg and test2.svg, the latter showing the spread-out result.

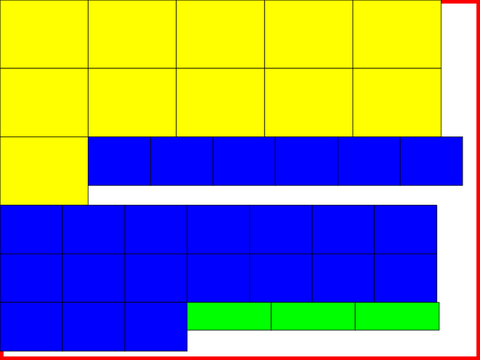
Here is an example how the output looks like (without the red border which is drawn to mark the pallet border):

arrange_spread2.py contains an adaption of arrange_spread.py for the actual problem.

Permutations without known length

When creating a layer out of articles of same height, then there are four strategies that I can choose from. It is four because there are two methods that I can either use or not. I can rotate the article by 90° per default or not and I can rotate the pallet or not.

So every time that I build a new layer, there are those four options. Depending on which strategy I choose, there is a different amount of possible leftover articles that did not fit into any layer. The amount is different because each strategy is more or less efficient.

To try out all combinations of possible layer arrangements, I have to walk through a tree where at each node I branch four times for each individual strategy. Individual neighboring nodes might be the same but this outcome is unlikely due to the path leading to those neighboring nodes being different.

To simplify, lets name the four possible strategies for each layers 0, 1, 2 and 3. I now want an algorithm that enumerates through all possible permutations of those four numbers for "some" length. This is similar to counting. And the itertools module comes with the product() method that nearly does what I want. For example, should I know that my tree does not become deeper than 8 (read: no more than eight layers will be built), then I can just run:

>>> for i in itertools.product([0,1,2,3], repeat=8):
...     print i
...
(0,0,0,0,0,0,0,0)
(0,0,0,0,0,0,0,1)
(0,0,0,0,0,0,0,2)
(0,0,0,0,0,0,0,3)
(0,0,0,0,0,0,1,0)
(0,0,0,0,0,0,1,1)
(0,0,0,0,0,0,1,2)
(0,0,0,0,0,0,1,3)

This would work if the number of layers created with each strategy was the same. But as each strategy behaves differently depending on the input, it cannot be known before actually trying out a sequence of strategies, how many layers it will yield.

The strategy (0,0,0,0,0,0,0,0) might create 7 layers, resulting in (0,0,0,0,0,0,0,1), (0,0,0,0,0,0,0,2) and (0,0,0,0,0,0,0,3) yielding the same output as only the first 7 strategies count. This would create duplicates which I should not waste cpu cycles on later.

It might also be that (0,0,0,0,0,0,1,0) turns out to be a combination of strategies that creates more than 8 layers in which case the whole thing fails.

So what I need is a generator, that gives me a new strategy depending on how often it is asked for one. It should dynamically extend the tree of possible permutations to accommodate for any size.

Since the tree will become humongous (4^11 = 4194304), already traversed nodes should automatically be cleaned so that only the nodes that make the current list of strategies stays in memory at any point in time.

This sounded all complicated which made me even more surprised by how simple the solution was in the end.

Here a version of the algorithm that could easily be ported to C:

class Tree:
    def __init__(self, branch_factor):
        self.branch_factor = branch_factor
        self.root = {"value": None, "parent": None, "children": []}
        self.current = self.root

    def next(self):
        if not self.current["children"]:
            self.current["children"] = [{"value":val, "parent":self.current, "children":[]} for val in range(self.branch_factor)]
        self.current = self.current["children"][0]
        return self.current["value"]

    def reset(self):
        if self.current["parent"]:
            self.current["parent"]["children"].pop(0)
        else:
            return False
        if self.current["parent"]["children"]:
            self.current = self.root
            return True
        else:
            self.current = self.current["parent"]
            return self.reset()

    def __str__(self):
        return str(self.root)

It would be used like this:

>>> tree = Tree(4)
>>> print tree.next(), tree.next(), tree.next()
>>> while tree.reset():
...     print tree.next(), tree.next(), tree.next()

Which would be equivalent to calling itertools.product([1,2,3,4], 3). The special part is, that in each iteration of the loop I can call tree.next() an arbitrary amount of times, just how much it is needed. Whenever I cannot generate an additional layer anymore, I can call tree.reset() to start a new permutation.

For my code I used a python specific version which is a generator:

def product_varlength(branch_factor):
    root = {"value": None, "parent": None, "children": []}
    current = root
    while True:
        if not current["children"]:
            current["children"] = [{"value":val, "parent":current, "children":[]} for val in range(branch_factor)]
        current = current["children"][0]
        if (yield current["value"]):
            while True:
                if current["parent"]:
                    current["parent"]["children"].pop(0)
                else:
                    return
                if current["parent"]["children"]:
                    current = root
                    break
                else:
                    current = current["parent"]

It is used like this:

it = product_varlength(4)
print it.next(), it.send(False), it.send(False)
while True:
    print it.send(True), it.send(False), it.send(False)

Again, the expression in the loop can have any number of it.send(False). The first it.send(True) tells the generator to do a reset.