enumerating elementary circuits of a directed_graph
Timestamp:
Tags:
code
For my GSoC project this year I need to be able to enumerate all elementary circuits of a directed graph. My code is written in Ocaml but neither the ocamlgraph library nor graph libraries for other languages seem to implement a well tested algorithm for this task.
In lack of such a well tested solution to the problem, I decided to implement a couple of different algorithms. Since it is unlikely that different algorithms yield the same wrong result, I can be certain enough that each individual algorithm is working correctly in case they all agree on a single solution.
As a result I wrote a testsuite, containing an unholy mixture of Python, Ocaml, D and Java code which implements algorithms by D. B. Johnson, R. Tarjan, K. A. Hawick and H. A. James.
Algorithm by R. Tarjan
The earliest algorithm that I included was published by R. Tarjan in 1973.
Enumeration of the elementary circuits of a directed graph
R. Tarjan, SIAM Journal on Computing, 2 (1973), pp. 211-216
http://dx.doi.org/10.1137/0202017
I implemented the pseudocode given in the paper using Python. The git repository can be found here: https://github.com/josch/cycles_tarjan
Algorithm by D. B. Johnson
The algorithm by D. B. Johnson from 1975 improves on Tarjan’s algorithm by its complexity.
Finding all the elementary circuits of a directed graph.
D. B. Johnson, SIAM Journal on Computing 4, no. 1, 77-84, 1975.
http://dx.doi.org/10.1137/0204007
In the worst case, Tarjan’s algorithm has a time complexity of O(n⋅e(c+1)) whereas Johnson’s algorithm supposedly manages to stay in O((n+e)(c+1)) where n is the number of vertices, e is the number of edges and c is the number of cycles in the graph.
I found two implementations of Johnson’s algorithm. One was done by Frank Meyer and can be downloaded as a zip archive. The other was done by Pietro Abate and the code can be found in a blog entry which also points to a git repository.
The implementation by Frank Meyer seemed to work flawlessly. I only had to add code so that a graph could be given via commandline. The git repository of my additions can be found here: https://github.com/josch/cycles_johnson_meyer
Pietro Abate implemented an iterative and a functional version of Johnson’s algorithm. It turned out that both yielded incorrect results as some cycles were missing from the output. A fixed version can be found in this git repository: https://github.com/josch/cycles_johnson_abate
Algorithm by K. A. Hawick and H. A. James
The algorithm by K. A. Hawick and H. A. James from 2008 improves further on Johnson’s algorithm and does away with its limitations.
Enumerating Circuits and Loops in Graphs with Self-Arcs and Multiple-Arcs.
Hawick and H.A. James, In Proceedings of FCS. 2008, 14-20
www.massey.ac.nz/~kahawick/cstn/013/cstn-013.pdf
In contrast to Johnson’s algorithm, the algorithm by K. A. Hawick and H. A. James is able to handle graphs containing edges that start and end at the same vertex as well as multiple edges connecting the same two vertices. I do not need this functionality but add the code as additional verification.
The paper posts extensive code snippets written in the D programming language. A full, working version with all pieces connected together can be found here: https://github.com/josch/cycles_hawick_james
The algorithm was verified using example output given in the paper. The project README states how to reproduce it.
Input format
All four codebases have been modified to produce executables that take the same commandline arguments which describes the graphs to investigate.
The first argument is the number of vertices of the graph. Subsequent arguments are ordered pairs of comma separated vertices that make up the directed edges of the graph.
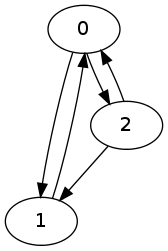
Lets look at the following graph as an example:
The DOT source for this graph is:
digraph G {
0;
1;
2;
0 -> 1;
0 -> 2;
1 -> 0;
2 -> 0;
2 -> 1;
}
To generate the list of elementary circuits using Tarjan’s algorithm for the graph above, use:
$ python cycles.py 3 0,1 0,2 1,0 2,0 2,1
0 1
0 2
0 2 1
The commandline arguments are the exact same for the other three methods and yield the same result in the same order.
If the DOT graph is in a format as simple as above, the following sed construct can be used to generate the commandline argument that represents the graph:
$ echo `sed -n -e '/^\s*[0-9]\+;$/p' graph.dot | wc -l` `sed -n -e 's/^\s*\([0-9]\) -> \([0-9]\);$/\1,\2/p' graph.dot`
Testsuite
As all four codebases take the same input format and have the same output format, it is now trivial to write a testsuite that compares the individual output of each algorithm for the same input and checks for differences.
The code of the testsuite is available via this git repository: https://github.com/josch/cycle_test
The other four repositories exist as submodules of the testsuite repository.
$ git clone git://github.com/josch/cycle_test.git
$ cd cycle_test
$ git submodule update --init
A testrun is done via calling:
$ ./test.sh 11
The argument to the shell script is an integer denoting the maximum number N
of vertices for which graphs will be generated.
The script will compile the Ocaml, Java and D sourcecode of the submodules as
well as an ocaml script called rand_graph.ml which generates random graphs
from v = 1..N vertices where N is given as a commandline argument. For each
number of vertices n, e = 1..M number of edges are chosen where M is
maximum number of edges given the number of vertices. For every combination of
number of vertices v and number of edges e, a graph is randomly generated
using Pack.Digraph.Rand.graph from the ocamlgraph library. Each of those
generated graphs is checked for cycles and written to a file graph-v-e.dot if
the graph contains a cycle.
test.sh then loops over all generated dot files. It uses the above sed
expression to convert each dot file to a commandline argument for each of the
algorithms.
The outputs of each algorithm are then compared with each other and only if they do not differ, does the loop continue. Otherwise the script returns with an exit code.
The tested algorithms are the Python implementation of Tarjan’s algorithm, the iterative and functional Ocaml implementation as well as the Java implementation of Johnson’s algorithm and the D implementation of the algorithm by Hawick and James.
Future developments
Running the testsuite with a maximum of 12 vertices takes about 33 minutes on a 2.53GHz Core2Duo and produces graphs with as much as 1.1 million cycles. It seems that all five implementations agree on the output for all 504 generated graphs that were used as input.
If there should be another implementation of an algorithm that enumerates all elementary circuits of a directed graph, I would like to add it.
There are some more papers that I would like to read but I lack access to epubs.siam.org and ieeexplore.ieee.org and would have to buy them.
Benchmarks seem a bit pointless as not only the algorithms are very different from each other (and there are many ways to tweak each of them) but also the programming languages differ. Though for the curious kind, it follows the time each algorithm takes to enumerate all cycles for all generated graphs up to 11 vertices.
| algorithm | time (s) |
|---|---|
| Johnson, Abate, Ocaml, iterative | 137 |
| Johnson, Abate, Ocaml, functional | 139 |
| Tarjan, Python | 153 |
| Hawick, D | 175 |
| Johnson, Meyer, Java | 357 |
The iterative Ocaml code performs as well as the functional one. In practice, the iterative code should probably be preferred as the functional code is not tail recursive. On the other hand it is also unlikely that cycles ever grow big enough to make a difference in the used stack space.
The Python implementation executes surprisingly fast, given that Tarjan’s algorithm is supposedly inferior to Johnson’s and given that Python is interpreted but the Python implementation is also the most simple one with the least amount of required datastructures.
The D code potentially suffers from the bigger datastructures and other bookkeeping that is required to support multi and self arcs.
The java code implements a whole graph library which might explain some of its slowness.